An interest rate swap is an over-the-counter (OTC) contract between two parties that agree to exchange cash flows on specified payment dates—one based on a variable (floating) interest rate and the other based on a fixed rate (the “swap rate”)—determined at the time the swap is initiated. The swap tenor is when the swap is agreed to expire.
Both interest rates are applied to the swap’s notional value to determine the size of each payment. Normally, the resulting two payments (one fixed, one floating) are in the same currency but will not be equal, so they are typically netted, with the party owing the greater amount paying the difference to the other party. In this manner, a party that currently has a fixed (floating) risk or other obligation can effectively convert it into a floating (fixed) one.
Interest rate swaps are among the most widely used instruments to manage interest rate risk. In particular, they are designed to manage the risk on cash flows arising from investors’ assets and liabilities. Interest rate swaps can be used to alter the duration of a fixed-income portfolio by changing a fixed-rate exposure to a floating-rate exposure, or vice versa.
A company with a floating-rate exposure can use a payer swap (pay fixed, receive floating) to change it into a fixed-rate exposure. The swap must have settlement dates that match the payment dates on the floating-rate liability.
Converting Floating to Fixed Using a Payer Swap
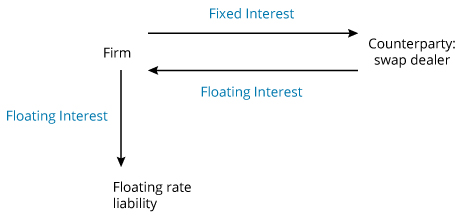
Note that the firm’s floating-rate payments from the swap will just offset its floating-rate payments on the liability, so the firm has only its fixed-rate liability from the swap.
Converting Fixed-Rate and Floating-Rate Exposures
| Existing Exposure | Converting | Interest Rate Swap Required | Beneficial When |
|---|---|---|---|
| Floating-rate liability | Floating to fixed | Payer swap | Floating rates expected to rise |
| Fixed-rate liability | Fixed to floating | Receiver swap | Floating rates expected to fall |
| Floating-rate asset | Floating to fixed | Receiver swap | Floating rates expected to fall |
| Fixed-rate asset | Fixed to floating | Payer swap | Floating rates expected to rise |
The notional principal of the interest rate swap to increase (or reduce) portfolio duration (target duration) can be calculated as follows:
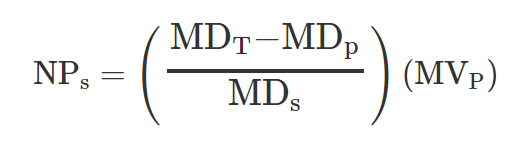
where:
NPS = notional swap principal
MDT = target modified duration
MDP = current portfolio modified duration
MDS = modified duration of swap
MVP = market value of portfolio
Interest Rate Forwards and Futures
The market in short-term interest rate derivatives is large and liquid, and the instruments involved are forward rate agreements (FRAs) and interest rate futures. A forward rate agreement is an OTC derivative instrument that is used mainly to hedge a loan expected to be taken out in the near future or to hedge against changes in the level of interest rates in the future.
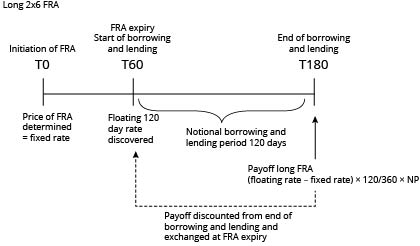
Consider a firm that anticipates borrowing a lump sum for 60 days, 30 days from now. The 60-day interest rate 30 days from now is uncertain. To hedge this uncertainty, the firm could take a long position in an FRA.
In general, managing short-term interest rate risk with an interest rate forward contract can also be done with an interest rate futures contract. Forwards, like swaps, are OTC instruments and are especially useful because they can be customized, but they do have counterparty risk. In contrast, exchange-traded interest rate futures contracts are standardized and guaranteed by a clearinghouse, so counterparty risk is virtually zero.
Institutional investors and bond traders can decide to use interest rate futures or fixed-income futures (also referred to as “bond futures”) contracts, which are longer dated, to hedge interest rate risk exposure. The choice will depend on the maturity of the bond or portfolio to be hedged.
FRA Diagram
Fixed-Income Futures
Portfolio managers that want to hedge the duration risk of their bond portfolios usually use fixed-income futures. They are standardized forward contracts listed on an exchange that have as underlying a basket of deliverable bonds with remaining maturities within a predefined range. The most liquid contracts include T-note and T-bond futures listed on the Chicago Board of Trade or the Chicago Mercantile Exchange.
A fixed-income futures contract has as its underlying reference assets a basket of deliverable bonds with a range of different coupon levels and maturity dates. Most futures contracts are closed before delivery or rolled into the next contract month. However, in the case of delivery, the futures contract seller has the obligation to deliver and the right to choose which security to deliver. For this reason, the duration of a futures contract is usually consistent with the forward behavior of the cheapest underlying deliverable bond. This is called the cheapest-to-deliver (CTD) bond, the eligible bond that the seller will most likely choose to deliver under the futures contract if he decides to deliver (rather than close out the futures position). The price sensitivity of the bond futures will, therefore, reflect the duration of the CTD bond.
To provide a guide for choosing the CTD bond, the concept of the conversion factor (CF) has been introduced.
The amount the futures contract seller receives at delivery will depend on the conversion factor that, when multiplied by the futures settlement price, will generate a price at which the deliverable bond would trade if its coupon were the notional coupon of the futures contract specification.
- Principal invoice amount = (Futures settlement price/100) × CF × Contract size.
The cheapest-to-deliver bond is determined on the basis of duration, relative bond prices, and yield levels. In particular, a bond with a low (high) coupon rate, a long (short) maturity, and thus a long (short) duration will most likely be the CTD bond if the market yield is above (below) the notional yield of the fixed-income futures contract. The notional yield is usually in line with the prevailing interest rate.
With futures we have to consider the cheapest-to-deliver bond price and the conversion factor.
By substituting into the equation ΔP = (HR)(ΔF), the hedge ratio becomes:
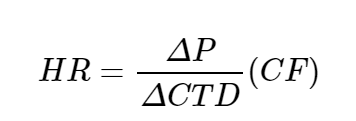
To fully hedge (immunize) a portfolio’s value against interest rate changes, the change in portfolio value must be offset by the change in the futures value:
- ∆P = HR × ∆ futures price

If the portfolio does not consist solely of the CTD bond, a duration-based hedge ratio (BPVHR) is calculated to determine the number of futures contracts required for a hedge:
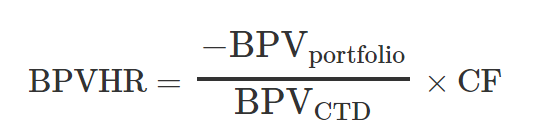
Basis point value (BPV) is the expected change in value of a security or portfolio given a one basis point (0.01%) change in yield.
BPV HR = number of short futures
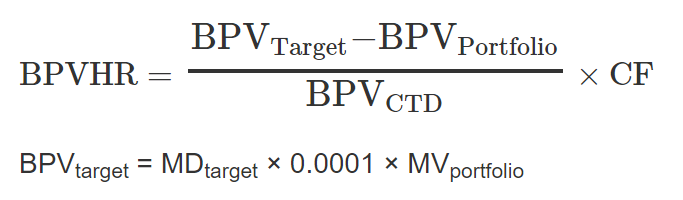
- BPVportfolio = MDportfolio × 0.01% × MVportfolio
MD = modified duration
- BPVCTD = MDCTD × 0.01% × MVCTD
- MVCTD = CTD price / 100 × $100,000
To achieve a target duration, the formula can be amended to:
In practice, hedging results are not perfect due to three main factors:
- The hedge was constructed using the CTD bond. If the level or slope of the term structure of interest rates changes significantly, the eligible bond, which is the CTD bond, may change. If the CTD bond changes, the duration of the Treasury bond future will also change.
- Duration is not a perfect measure of how bond prices react to interest rate changes. Duration ignores the convexity of the bonds.
- Modified duration only captures the impact of parallel movements in the term structure of interest rates. Shaping risk refers to nonparallel changes in the term structure, such as steepening, flattening, and changes in curvature.
