The active return (RA)—of an actively managed portfolio is driven by the difference in weights between the active portfolio and the benchmark:
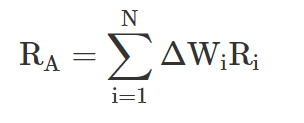
where:
Ri = the return from security i
ΔWi = the active weight, the difference between portfolio and benchmark weight, for security i
Conceptually, a manager can generate active returns by
- strategically adjusting the active weights of the securities to create long-term exposures to rewarded risks that are different from those of his benchmark
- tactically adjusting the active weights of the securities using his skills/expertise in identifying mispricing in securities, sectors, rewarded risks, and so on, to generate alpha that cannot be explained by long-term exposure to rewarded risks
- assuming excessive idiosyncratic risk that may result in lucky or unlucky returns. It is labeled luck in the sense that it is not due to market risk exposure or value-added alpha.
The decomposition of realized (ex post) active return can be seen in the next equation:
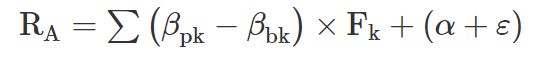
where:
where
βpk = the sensitivity of the portfolio (p) to each rewarded factor (k)
βbk = the sensitivity of the benchmark to each rewarded factor
Fk = the return of each rewarded factor
(α + ε) = the return not explained by exposure to rewarded factors—alpha (α) is the active return attributable to manager skill, and ε is the idiosyncratic return—noise or luck (good or bad)
