Put-Call Parity and Synthetic Positions
Put-call parity is the principle used to generate synthetic longs and shorts. The equation equates the value of a protective put (long stock, long put) with the value of a long call option + the PV of a zero-coupon bond with a face value at the strike price.
- S0 + P0 = C0 + PV(X)
If we rearrange this equation, we can isolate terms and see how synthetic instruments are equivalent to a desired position.
For example, a synthetic call is equivalent to C = S + P – PV(X). In words, a synthetic call is equal to a long position in a stock, as long put and short position in a zero-coupon bond. The short bond position represents borrowing money to pay for the cost of the position.
- A Put option then, is P = C – S + PV, meaning we long a call but short the underlying.
Option Binomial Trees
We can apply binomial trees to calculate the value of options. Options generate tree paths by the 2 states that can occur, an up value and a down value. To calculate the value of the option, we first adjust the up and down values in to risk neutral probability rates. If not given, the up and down factors can be calculated as:
- up factor is u = S+/S
- down factor d = S-/S
The risk neutral up probability is:

- And down factor probability is 1- up factor probability.
With these probabilities, the next step is to construct the binomial tree with the profit values and price values. To do so we find the S+ and S- terms, as well as the C+ and C- terms.
- S+ = Spot Price x Up Factor
- S- = Spot Price – Down Factor
- C+ = max profit given S+
- C- = Max profit given S-
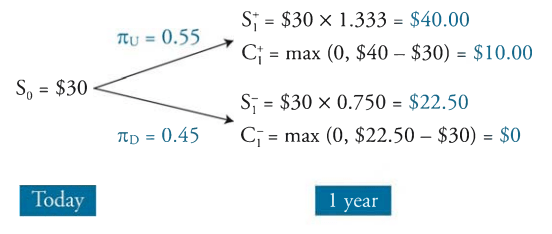
The expected value of the option is then
- (C+ x Up probability) + (C– x Down Probability)
To get the PV we discount by Rf.
This concept can be applied to multiperiod options as well.
Arbitrage Hedge Ratio
Suppose that the price of an option differs from what is calculated by the binomial model, creating an arbitrage opportunity. If the option is overpriced, to profit, we would sell the option and by a fractional share of the underlying per each option sold. If the option is underpriced, we would by the option and short a fractional amount of the underlying. To calculate that fractional amount, we use the hedge ratio or delta ratio.
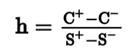
BSM & Dynamic Delta Hedging
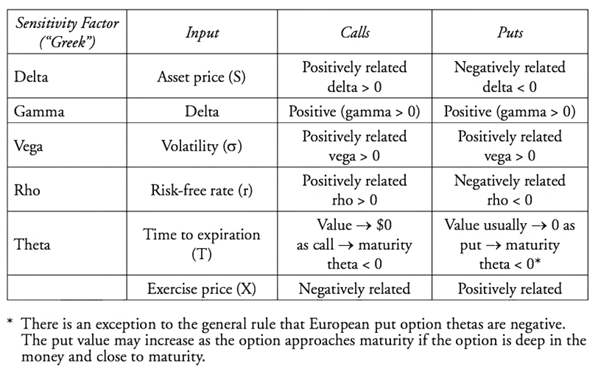
The Black-Scholes Model allows continuous or “live” pricing of options based on the values of “Option Greeks.” The Greeks are factors of option prices, called Delta, Gamma, Vega, Rho and Theta. Delta represents the price of the underlying asset, Gamma is the change the rate of Change in Delta, Vega is volatility, Rho is the risk-free rate and theta represents time to expiration. Changes in each Greek will impact the price of calls and puts. Call values are positively related to the Greeks, but Puts are split in that Delta and Rho are negatively related to the value of the put.
Dynamic Delta hedging is as a method of combining short call options with long stock positions so that the value of the portfolio does not change as the value of the stock changes. The hedge can also be accomplished by combing accomplished by longing a put and longing the underlying stock.
- Number of short calls needed = Number of shares hedged/Delta of call option
- Number of long puts needed = Number of shares hedged/Delta of put option
The hedge is considered dynamic because it only holds for small changes in stock price, meaning the hedge requires constant rebalancing to be maintained.
