How to use a binomial interest rate tree to find bond prices
One method that we use to value bonds under the arbitrage-free model performing backwards induction on binomial interest rate trees. An interest is a calibrated framework that starts with a spot rate and generates and up and down rate branches based on interest volatility estimates. The rates are calibrated to match market prices, which is usually done by computer as it is a tedious process.
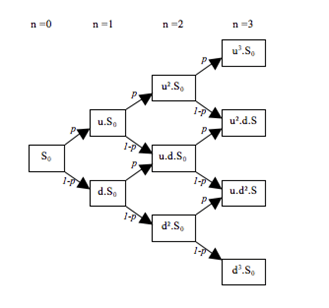
A correctly calibrated interest rate tree will conform to the following rules:
- The rates will generate arbitrage free prices for the benchmark security.
- Forward rates are 2 standard deviations apart, allowing us to compute other rates given one
- The middle forward rate in a period is approximately equal to the implied one period forward rate for that period.
Calculating the value of a bond using binomial tree is possible because we know that the amount that the last payment will be (FV + Coupon). Thus, we can discount by the previous period rate given and compute the PV of the previous period bond.
Now, this previous period value will have two branches, and so will be comprised of probability weighted sum of the two possible expected values, calculated using the up rate and the down rate. With this method, we can discount all the way back to time 0, and this gives us the PV of the bond.


For example, given the above chart and assuming our bond is a risk-free 2.8% coupon bond, we can find the value of the bond at Year 2 using backwards induction. We start with the final year three cash flow of 102.8 and induct backwards assuming a 50% probability of either an up and down rate.
Note that we are adding 2.8 for Vuu and Vu calculations because the PV would include a beginning period coupon which is already at its PV. We could also skip the first Vuu coupon, but in that case we would need to add to our Vu calculation.
ie) (101.117 + 2.8)/1.0


Alternatively, we could calculate Value at Year 2 as 104/1.045 = 99.52, but the value at year one we would need to add the coupon back, giving us a node value of (99.52+4)/1.0360.
We can also be given an OAS, be sure to add this to rate in order to calculate the market price of bond if that is being asked for.
Putable and Callable Bonds
We can translate this binomial model to help us value bonds with options as well. The only difference to account for is that we will need to adjust value to the exercise value for bonds that hit the exercise price.

