Decision Theory
Decision theory is concerned with identifying values, probabilities, and other uncertainties relevant to a given decision and using that information to arrive at a theoretically optimal decision. Decision theory is normative, meaning that it is concerned with identifying the ideal decision.
Development of Normative Decision Theory—Timeline

In order to take SEU theory and apply it to actual decision making, prescriptive theories of choice should consider the empirical evidence as to how people actually make decisions.
Prescriptive approaches based on SEU theory consider empirical evidence as to the limits on human rationality. These limitations are imposed by the complexity of the world we live in, the incompleteness and inadequacy of human knowledge, the computational inadequacy of people, the inconsistencies of individual preference and beliefs, and the conflicts of value among individuals and groups.
Bounded Rationality
Descriptive analysis of problem solving and decision making are centrally concerned with how people manage to reduce complicated problems to a cognitively manageable size, with how they approximate and heuristically handle complexity. Descriptive analyses make it possible to develop theories and practices that account for the unrealistic parts of SEU theory.
These theories illustrate how people respond to complexity and limitations, while striving to achieve results that approximate the ideal (i.e., the results of normative theories). Bounded rationality and prospect theory are examples of such theories
Bounded rationality assumes knowledge capacity limits and removes the assumptions of perfect information, fully rational decision-making, and consistent utility maximization. Individuals instead practice satisfice. Limitations imposed by cost and time result in outcomes that offer sufficient satisfaction rather than optimal utility. Individuals operate with partial information and use heuristics (mental shortcuts) to process the information.
Bounded rationality acknowledges it is impractical to consider all potential outcomes. As an alternative to optimization, individuals set constraints that will lead to a satisfactory outcome. Individuals use experience and the observation of others to set aspiration levels. Aspiration levels are then adjusted upward if previous aspirations are met, and downward if they are not.
Prospect Theory
Prospect theory describes how individuals make choices in situations in which they have to decide between alternatives that involve risk (e.g., financial decisions) and how individuals evaluate potential losses and gains. Prospect theory considers how prospects (alternatives) are perceived based on their framing, how gains and losses are evaluated, and how uncertain outcomes are weighted.
Under prospect theory, choices are made in two phases. In the first phase, the editing phase, proposals are framed or edited using simple heuristics (decision rules) to make a preliminary analysis prior to the second evaluation phase.
The sequence of editing operations is likely to vary with the offered set and the format of the display. In the editing phase, a decision maker organizes and reformulates the available options to simplify the choice.
- Codification: People perceive outcomes as gains and losses rather than final states of wealth or welfare. A gain or loss is, of course, defined with respect to some reference point. The location of the reference point affects whether the outcomes are coded as gains or losses. Prospects are coded as (gain or loss, probability; gain or loss, probability; …) such that the probabilities initially add to 100 percent or 1.0.
- Combination: Prospects are simplified by combining the probabilities associated with identical gains or losses. For example, a prospect initially coded as (250, 0.20; 200, 0.25; 200, 0.15; 150, 0.40) will be simplified to (250, 0.20; 200, 0.40; 150, 0.40).
- Segregation: The riskless component of any prospect is separated from its risky component. For example, a prospect initially coded as (300, 0.8; 200, 0.2) is decomposed into a sure gain of (200, 1.0) and a risky prospect of (100, 0.8; 0, 0.20). The same process is applied for losses.
The above operations are applied to each prospect separately. The following operations are applied to two or more prospects:
- Cancellation: Cancellation involves discarding common outcome probability pairs between choices. For example, the pairs (200, 0.2; 100, 0.5; 20, 0.3) and (200, 0.2; 300, 0.4; –50, 0.4) are reduced to (100, 0.5; 20, 0.3) and (300, 0.4; –50, 0.4).
- Simplification: Prospects are likely to be rounded off. A prospect of (51, 0.49) is likely to be seen as an even chance to win 50. Also, extremely unlikely outcomes are likely to be discarded or assigned a probability of zero.
- Detection of Dominance: Outcomes that are strictly dominated are scanned and rejected without further evaluation.
Editing choices can sometimes lead to the preference anomaly known as the isolation effect, where investors focus on one factor or outcome while consciously eliminating or subconsciously ignoring others. It is referred to as an anomaly because the sequence of the editing can lead to different decisions.
In the second phase, the evaluation phase, investors focus on loss aversion rather than risk aversion. The difference is subtle, but the implication is that investors are more concerned with the change in wealth than they are in the resulting level of wealth, per se.
In the evaluation phase, investors place values on alternatives in terms of weighted and probability-weighted outcome to determine expected utility. The equation is shown as:
- utility = w(p1)v(X1) + w(p2)v(X2) + …
where:
p1 and p2 = probability weights of possible outcomes X1 and X2
v = a function that assigns value to an outcome
w = a probability weighting function
The important implications are:
- w reflects a tendency of individuals to overreact to small probabilities and underreact to large probabilities.
- The value function is based on changes and is not level.
Value Function
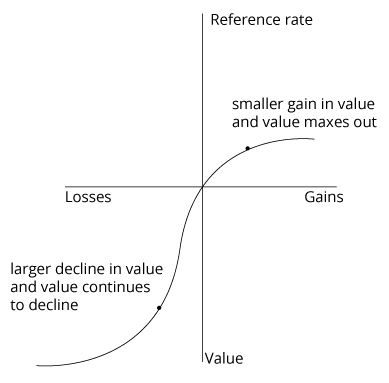
The conclusion is that individuals are risk averse when facing choices with a high probability of gains and low probability of losses. However, individuals display risk-seeking behavior when confronted with choices that lead to a high probability of losses and a low probability of gains.
