Effects of Currency on Portfolio Risk and Return

Domestic currency or home currency is the currency of the investor (or the currency in which portfolio results are reported and analyzed).

Domestic asset is an asset denominated in the investor’s domestic currency.

Foreign currency and foreign asset are a currency other that the investor’s domestic currency and an asset denominated in that foreign currency. These are sometimes called the local currency and local market, respectively.

Foreign-currency return (R_FC) is the return of the foreign asset measured in its local (foreign) currency. It can be called the local market return.

The percentage change in value of the foreign currency is denoted as R_FX. It can be called the local currency return.

Domestic-currency return (R_DC) is the return in domestic currency units considering both the foreign-currency return (R_FC) and the percentage change in value of the foreign currency (R_FX).

Return Decomposition

The domestic-currency return is multiplicative with respect to these two factors:

• R_DC = (1 + R_FC)(1 + R_FX) – 1  

where:

R_DC is the domestic-currency return (in percent)

R_FC is the foreign-currency return

R_FX is the percentage change of the foreign currency against the domestic currency.

There are three ways to calculate R_DC:

• R_DC ≈ R_FC + R_FX: This approach is an approximation of the more accurate compounded calculation. It emphasizes the two sources of return, R_FC and R_FX. It is acceptable when precision is not needed, such as selecting between three quite different multiple choice answers or discussing the theoretical sources of return.
• R_DC = (1 + R_FC)(1 + R_FX) – 1 = R_FC + R_FX + (R_FC)(R_FX): This approach is precise if the precise R_FX is known. I would generally use this approach, unless given clear reasons to do something else.
• However, there are cases where determining R_FX is not simple. If the currency is hedged, then a precise currency hedge must short the ending number of foreign currency units; however, that ending number is not knowable for a risky asset. You will see a naïve hedge is normally used and the beginning number of foreign currency units are sold forward. In that case, a simple comparison of Fo and So will not be the true R_FX. In that case, you will see a different set of calculations made. You would directly calculate beginning and ending value of the portfolio in the investor’s domestic currency units. Then R_DC is (EV – BV) / BV.

What holds for the domestic-currency return of a single foreign asset also holds for the returns on a multi-currency portfolio of foreign assets, except now the portfolio weights must be considered. More generally, the domestic-currency return on a portfolio of multiple foreign assets will be equal to:

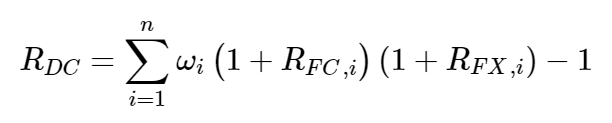
where: 

R_FC,i is the foreign-currency return on the i-th foreign asset

R_FX,i is the appreciation of the i-th foreign currency against the domestic currency

ω_i are the portfolio weights of the foreign-currency assets (defined as the percentage of the aggregate domestic-currency value of the portfolio)

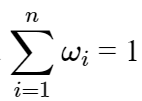
Alternatively:

Volatility Decomposition

Now we will turn to examining the effect of currency movements on the volatility of domestic-currency returns. Start by rearranging the equation above:

• R_DC = (1 + R_FC)(1 + R_FX) – 1 = R_FC + R_FX + R_FCR_FX

When R_FC and R_FX are small, then the cross-term (R_FCR_FX) is small, and as a result this equation can be approximated as:

• R_DC ≈ R_FC + R_FX  

We can combine the that with the statistical rule that:

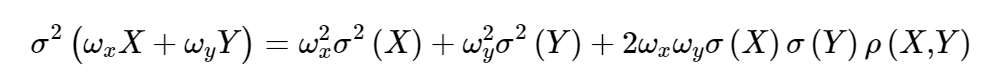
where 

X and Y are random variables

ω are weights attached to X and Y

σ² is variance of a random variable

σ is the corresponding standard deviation

ρ represents the correlation between two random variables

Applying this result to the domestic-currency return approximation leads to:

• σ²(R_DC) ≈ σ²(R_FC) + σ²(R_FX) + 2σ(R_FC)σ(R_FX)ρ(R_FC,R_FX)  

This equation is for the variance of the domestic-currency returns (R_DC), but risk is more typically defined in terms of standard deviation because mean and standard deviation are measured in the same units (percent, in this case).

Hence, the total risk for domestic-currency returns—that is, σ(R_DC)—is the square root of the results calculated above.

Examining the equation indicates risk to our domestic investor:

• Depends on the standard deviation of R_FC and R_FX.
• May be higher for our domestic investor because standard deviation of R_FX is an additive term in the equation.
• However, correlation also matters. If the correlation between R_FC and R_FX is negative, the third component of the calculation becomes negative. The correlation measures the interaction of R_FC and R_FX.
  • If the correlation is positive, then R_FC returns are amplified by R_FX returns, increasing the volatility of return to our domestic investor.
  • If the correlation is negative, then R_FC returns are dampened by R_FX returns, decreasing the volatility of return to our domestic investor. (This is discussed further under this reading’s topic of minimum variance hedge ratio).

If R_FC is a Risk-Free Return: In this case, its standard deviation and correlation with R_FX are zero. When R_FX is the only source of risk for the domestic investor in the foreign asset, a direct and precise calculation of the standard deviation of R_DC is practical.

• Equation 4: σ(R_DC) = σ(R_FX)(1 + R_FC)

where:

R_FC = the return on a foreign currency denominated risk-free asset

Table of Contents