Immunizing Multiple Liabilities

The principle of interest rate immunization applies to multiple liabilities in addition to a single liability. 

There are several approaches to manage Type I Liabilities:

• Cash flow matching, which entails building a dedicated portfolio of zero-coupon or fixed-income bonds to ensure that there are sufficient cash inflows to pay the scheduled cash outflows;
• Duration matching, which extends the ideas of the previous section to a portfolio of debt liabilities;
• Derivatives overlay, in particular using futures contracts on government bonds in the immunization strategy; and
• Contingent immunization, which allows for active bond portfolio management until a minimum threshold is reached and that threshold is identified by the interest rate immunization strategy.

Cash Flow Matching

Cash flow matching is the safest approach. In some cases, this may allow accounting defeasance where the assets are legally set aside and dedicated to meet the liabilities—allowing both those assets and liabilities to be removed from the balance sheet of the organization responsible for paying the liability. The simplest cash flow match is to buy zero-coupon bonds in the amounts and due dates to meet each liability.

• Cash flow matching of a stream of liabilities may also be possible using coupon-bearing bonds.
• In practical terms, it is unlikely that the coupon-bearing bonds necessary for perfect cash flow matching will exist. A cash-in-advance constraint could be used, requiring the bond used to fund a specific liability to mature before the required payout date of the liability. This would expose the portfolio to reinvestment risk in an upward-sloping yield curve. The upward-sloping curve is anticipated to create reinvestment risk because as cash comes in to be reinvested for a short time period until payout, the reinvestment must be at the lower rates at the short end of the curve.

Duration Matching

Duration matching is a more flexible and generally practical approach to funding multiple liabilities. Like immunizing a single liability, there must be sufficient assets to fund the liability, and Macaulay durations of assets and liabilities (in this case, the average liability duration) must match.

However, matching money durations is the more common approach. Money duration is more useful when initial amounts and discount rates of assets and liabilities differ. The rules for immunizing multiple liabilities become the following:

1. Initial portfolio market value (PVA) equals (or exceeds) PVL. (There are exceptions to this for some situations where the initial portfolio IRR differs from the initial discount rate of the liability.)
2. Portfolio and liability basis point values match (BPV = BPV_L).
3. Asset dispersion of cash flows and convexity exceed those of the liabilities. (But not by too much, in order to minimize structural risk exposure to curve reshaping).
4. Regularly rebalance the portfolio to maintain the BPV match of A and L as time and yields change.

Derivatives Overlay (Managing a Duration Gap)

A derivatives overlay can be used to adjust the portfolio and maintain the duration match without the expense of adjusting the underlying assets. Futures contracts are often used.

In the United States, there are various Treasury futures contracts available based on the 30-year bond, as well as 2-, 5-, and 10-year Treasury notes. Each contract specifies a set of deliverable securities that the contract seller may deliver at contract expiration. The seller must deliver 100,000 par of a deliverable security [also called most deliverable bond or cheapest to deliver (CTD) bond]. The buyer must pay the seller the initial contract price multiplied by the conversion factor for that bond (CF_CTD) that the seller chooses to deliver.

The issue of which bond the seller chooses to deliver is important because the duration of that CTD determines the duration (price volatility) of the contract—hence, its BPV. The exact calculation of contract BPV is complex, but is approximately:

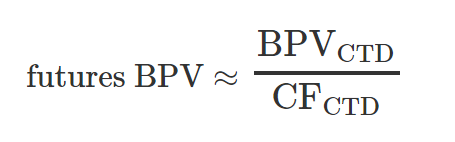
Calculating the number of contracts required to adjust the portfolio assets is simply the desired change in BPV divided by the BPV of the contract:

Contingent Immunization

Contingent immunization (CI) is a hybrid active/passive strategy and requires a significant surplus. As long as that surplus is of sufficient size, the portfolio can be actively managed. At the extreme, assets could be invested in equity, commodities, real estate, or any other assets.

If the assets earn more than the initially available immunization rate, the surplus will grow, and can eventually be returned to the investor. If the strategy is unsuccessful, the surplus will shrink, and the portfolio must be immunized before the surplus declines below zero. For example:

• Invest the entire portfolio in stocks.
• Invest only the surplus in stocks or in long stock options. Use the balance of the assets to construct an immunized portfolio. This approach allows fewer funds for active management, but is in some ways safer because only the surplus amount is at risk of loss, and an immunized portfolio is already in place.
• Use active bond management techniques. The manager could overhedge or underhedge based on a view of interest rates.
  • If the manager believes rates will increase, underhedge (<100%) and the losses on the contracts will be reduced, improving portfolio performance and increasing the surplus.
  • If the manager believes rates will decrease, overhedge (>100%) and the gains on the contracts will be increased, improving portfolio performance and increasing the surplus.
  • Because the contract is based on 100,000 par, each 1/32 of change in price of 100 par will equate directly to a gain or loss on the contract of 31.25 [(1 / 32) × (100,000 / 100)].

CI approaches can be vulnerable to liquidity risk.

• If all of the assets (instead of just the surplus) are actively managed and the surplus declines, the assets must be quickly liquidated without further loss and converted to an immunizing portfolio before the surplus becomes negative.
• Even if only the surplus amount is actively managed, liquidity issues can still be a problem. If short option contracts were used, the downside risk is unlimited for calls and very large for puts (in excess of initial premiums received). Likewise, the potential losses on futures contracts are very large and could exceed the portfolio surplus.

Table of Contents