An interesting connection among the portfolio convexity, Macaulay duration, dispersion, and cash flow yield:
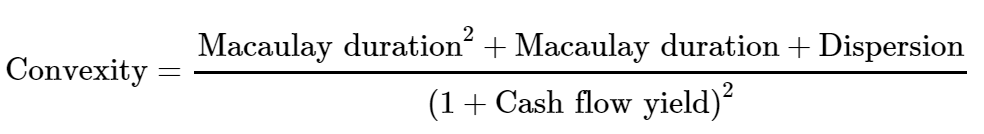
The portfolio dispersion and convexity statistics are used to assess the structural risk to the interest rate immunization strategy. Structural risk arises from the potential for shifts and twists to the yield curve. This risk is discussed later in this section.
An immunization strategy is essentially “zero replication.” We know that the perfect bond to lock in the six-year holding period rate of return is a six-year zero-coupon bond having a face value that matches the EUR 250 million liability. The idea is to originally structure and then manage over time a portfolio of coupon-bearing bonds that replicates the period-to-period performance of the zero-coupon bond. Therefore, immunization is essentially just an interest rate hedging strategy. As the yield on the zero-coupon bond rises and falls, there will be unrealized losses and gains.
In below, this is illustrated by the zero-coupon bond’s value moving below and above the constant-yield price trajectory. Two paths for the zero-coupon yield are presented: Path A for generally lower rates (and higher values) and Path B for higher rates (and lower values). Regardless, the market value of the zero-coupon bond will be “pulled to par” as maturity nears.
Immunizing with coupon-bearing bonds entails continuously matching the portfolio Macaulay duration with the Macaulay duration of the zero-coupon bond over time and as the yield curve shifts, even though the zero-coupon bond could be hypothetical and not exist in reality. .
Also, the bond portfolio’s initial market value has to match or exceed the present value of the zero-coupon bond. The Macaulay duration of that, perhaps hypothetical, zero-coupon bond always matches the investment horizon. Immunization will be achieved if any ensuing change in the cash flow yield on the bond portfolio is equal to the change in the yield to maturity on the zero-coupon bond.
That equivalence will ensure that the change in the bond portfolio’s market value is close to the change in the market value of the zero-coupon bond. Therefore, at the end of the six-year investment horizon, the bond portfolio’s market value should meet or exceed the face value of the zero-coupon bond, regardless of the path for interest rates over the six years.
