Active yield curve strategies are designed to capitalize on expectations regarding the level, slope, or shape (curvature) of yield curves.
A yield curve shows the yield as a function of maturity (or sometimes of duration) for otherwise comparable bonds.
Yield curves are most typically plotted for credit risk-free government bonds because they are generally available for a wide range of maturities and do not introduce the additional complexity of changes in credit spread. The “yield” could be yield-to-maturity (YTM), spot rates, or even forward rates.
Yield curves are generally not stable but change over time. To determine how to profit from expected changes in the yield curve, it is helpful to view yield curve changes as resulting from three sources. Change in:
Level: A parallel shift where all yields shift up (or down) by the same amount.
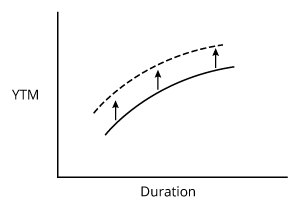
Slope: Where the curve becomes flatter or steeper.
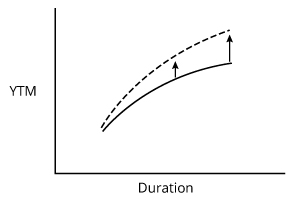
Curvature: Where the curve becomes more like a straight or curved line.
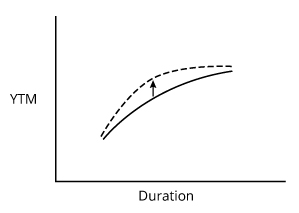
In reality, most changes in the curve involve more than one source.
Duration and Convexity
Review of various duration measures:
Macaulay duration is analogous to a bond’s effective maturity, incorporating all of the bond’s projected cash flows—both principal and interest. It is a weighted average of time to receive the bond’s promised payments. The present value of each payment to be received is weighted by the present value of all future payments.
Modified duration provides a more direct measure of the relationship between changes in a bond’s yield and percentage changes in its price. Modified duration is the Macaulay duration statistic divided by one plus the yield to maturity for each period.
It provides an estimate of the percentage price change for a bond given a 1% (100 bps) change in its yield to maturity. It is important to remember that modified duration estimates the percentage price change of the full price, including accrued interest.
Effective duration is the sensitivity of a bond’s price to a change in a benchmark yield curve (as opposed to the price response to a change in the bond’s own yield, which might result from factors other than changes in the benchmark yields).
Effective duration is similar to modified duration, but its calculation is flexible to allow its use in cases when the bond has an embedded option. As an example, a callable bond has cash flows that are contingent on future interest rates. The issuer may call the bond as interest rates fall—depending on its ability to refinance the debt. Such a bond does not have well-defined cash flows to plug into the modified and Macaulay duration calculations.
Key rate duration (also called partial duration, or partials) is a measure of a bond’s sensitivity to a change in the benchmark yield curve at a specific maturity point or segment.
Key rate durations help identify “shaping risk” for a bond or a portfolio—that is, its sensitivity to changes in the shape of the benchmark yield curve (e.g., the yield curve becoming steeper or flatter, or showing more or less curvature).
The money duration of a bond is a measure of the price change in units of the currency in which the bond is denominated. Money duration can be stated per 100 of par value or in terms of the bond’s actual position size in the portfolio. In the United States, money duration is commonly called “dollar duration.”
The price value of a basis point (PVBP) is an estimate of the change in a bond’s price given a 1 bp change in yield to maturity. PVBP “scales” money duration so that it can be interpreted as money gained or lost for each basis point change in the reference interest rate.
This measure is also referred to as the “dollar value of an 0.01” (pronounced oh-one) and abbreviated as DV01. It is calibrated to a bond’s par value of 100.
Duration is a first-order effect that attempts to capture a linear relationship between bond prices and yield to maturity.
Convexity is a second-order effect that describes a bond’s price behavior for larger movements in yield. It captures the extent to which the yield/price relationship deviates from a linear relationship. If a bond has positive convexity, then the bond price increases more if interest rates decrease (and decreases less if interest rates increase) than the duration estimate would suggest. Said another way, the expected return of a bond with positive convexity will be higher than the return of an identical-duration, lower-convexity bond if interest rates change. This price behavior is valuable to investors, and therefore a bond with higher convexity might be expected to have a lower yield than a similar-duration bond with less convexity.
Although convexity is valuable when interest rates are expected to change, it is likely to be even more valuable when interest rate volatility is expected to increase. This dynamic tends to drive changes in the shape of the yield curve—as convexity becomes more valuable, investors will bid up prices on the longer-maturity bonds (which have more convexity), and the long end of the curve may decline or even invert (or invert further), increasing the curvature of the yield curve.
Macaulay duration and modified duration cannot be used to measure the price risk of securities whose cash flows change when interest rates change. Similarly, nominal convexity calculations assume that the cash flows do not change when yields change.
Effective convexity, like effective duration, uses a methodology that can accommodate cash flows that change when yields change (as in the case of callable bonds or mortgage-backed securities [MBS]). This measure is used when describing the price behavior of bonds with embedded options.
A helpful heuristic for understanding convexity is that, for zero-coupon bonds:
- Macaulay durations increase linearly with maturity—a 30-year zero-coupon bond has three times the duration of a 10-year zero-coupon bond.
- Convexity is approximately proportional to duration squared; therefore, a 30-year zero-coupon bond has about nine times the convexity of a 10-year zero-coupon bond.5
- Coupon-paying bonds have more convexity than zero-coupon bonds of the same duration—a 30-year coupon-paying bond with a duration of approximately 18 years has more convexity than an 18-year zero-coupon bond.6 The more widely dispersed a bond’s cash flows are around the duration point, the more convexity it will exhibit. For this reason, a zero-coupon bond has the lowest convexity of all bonds of a given duration.
Although convexity can be a valuable tool when positioning a portfolio, it is important to remember that convexity is a second-order effect; it operates behind duration in importance and can largely be ignored for small yield changes. When convexity is added with the use of derivatives, however, it can be extremely important to returns. This effect will be demonstrated later in this reading. Negative convexity may also be an important factor in a bond or portfolio’s returns. For bonds with short options positions embedded in their structures (such as MBS or callable bonds) or portfolios with short options positions, convexity’s effect may be large.
Adding convexity to a portfolio is not free: Portfolios with higher convexity are most often characterized by lower yields. Investors will be willing to pay for increased convexity when they expect yields to change by more than enough to cover the give-up in yield. Convexity is more valuable when yields are more volatile.
A portfolio’s convexity can be altered by shifting the maturity/duration distribution of bonds in the portfolio, by adding physical bonds with the desired convexity properties, or by using derivatives.
