Liability-relative asset allocation is aimed at the general issue of rendering decisions about asset allocation in conjunction with the investor’s liabilities. Liability-relative investors view assets as an inventory of capital, sometimes increased by additions, which is available to achieve goals and to pay future liabilities.
The following characteristics of liabilities are relevant to the asset allocation decision:
- Fixed versus contingent: Fixed liabilities have cash flows whose amount and timing are specified in advance, such as a fixed-rate corporate bond. Contingent liabilities have cash flows that depend on uncertain future events, such as the pension liability associated with a defined pension plan.
- Legal versus quasi-legal: Legal liabilities are obligations defined in a legal agreement. Quasi-legal liabilities are not legal obligations but are cash outflows expected to occur in the future and are essential to the mission of the institution. University endowments can be considered to have quasi-legal liabilities.
- Duration and convexity measure the change in value of a liability for a given change in interest rates. In the CFA curriculum, we typically talk about duration and convexity in relation to fixed-income securities, but the concept can be applied to any liability.
- Liability value versus size of sponsoring organization: A large liability in relation to the size of the sponsoring organization will necessarily be accounted for in the asset allocation decision; a small liability can usually be ignored as its effect on the optimal asset allocation is minimal.
- Factors that affect future cash flows: These factors include inflation, interest rates, risk premiums, and other economic conditions. DB pension obligations are influenced by the choice of the discount rate, for example.
- Timing considerations, including longevity risk.
- Regulations affecting the determination of the liability’s value, typically found in the insurance industry.
Various approaches to liability-relative asset allocation exist. These methods are influenced by tradition, regulations, and the ability of the stakeholders to understand and extend portfolio models that come from the asset-only domain.
- Surplus optimization: This is an extension of MVO in which we determine an efficient frontier based on the surplus with its volatility as our measure of risk, stated either in money or percentage terms.
- Two-portfolio approach: In this approach, we separate the asset portfolio into two subportfolios: a hedging portfolio and a return-seeking portfolio.
- Integrated asset-liability approach: This approach integrates both the assets and the liabilities in a joint optimization method.
Surplus Optimization
Surplus optimization involves adapting asset-only mean–variance optimization by substituting surplus return for asset return over any given time horizon. The quadratic optimization program involves choosing the asset allocation (mix) that maximizes expected surplus return net of a penalty for surplus return volatility at the chosen time horizon. The objective function is
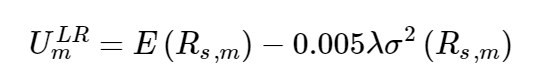
where:
E(Rs,m) = expected surplus return
Vars,m = variance of surplus return
The following steps describe the surplus optimization approach:
- Select asset categories and determine the planning horizon. One year is often chosen for the planning exercise, although funding status analysis is based on an analysis of all cash flows.
- Estimate expected returns and volatilities for the asset categories and estimate liability returns (expanded matrix).
- Determine any constraints on the investment mix.
- Estimate the expanded correlation matrix (asset categories and liabilities) and the volatilities.
- Compute the surplus efficient frontier and compare it with the asset-only efficient frontier.
- Select a recommended portfolio mix.
Two-Portfolio Approach (Hedging or Return-Seeking Approach)
In this approach, we create an asset portfolio that hedges the liabilities, and the remainder is managed independently using MVO to maximize utility and identify the optimal risk-return tradeoff.
The hedging portfolio can be created using the various techniques such as cash flow matching, duration matching, and immunization.
This approach can be modified by only partially hedging the liabilities and allocating more capital to the return-seeking portfolio or increasing the allocation to the hedging portfolio as the funding ratio and the surplus increase. Both of these approaches are more aggressive than completely hedging the liabilities, as they trade off higher expected return for higher risk.
There are two limitations of this approach:
- If the funding ratio is less than one, it’s difficult to create a hedging portfolio that completely hedges the liabilities.
- A hedging portfolio may not be available to hedge certain kinds of risk.
Integrated Asset-Liability Approach
Banks, hedge funds with short positions, and insurance companies, however, make decisions about the composition of their liabilities jointly with their asset allocation decisions. There is a continuous feedback loop between the two, which requires a multiperiod model. This is often referred to as an integrated asset-liability approach.
Characteristics of the Three Liability-Relative Asset Allocation Approaches
| Surplus Optimization | Hedging/Return-Seeking Portfolios | Integrated Asset–Liability Portfolios |
|---|---|---|
| Simplicity | Simplicity | Increased complexity |
| Linear correlation | Linear or non-linear correlation | Linear or non-linear correlation |
| All levels of risk | Conservative level of risk | All levels of risk |
| Any funded ratio | Positive funded ratio for basic approach | Any funded ratio |
| Single period | Single period | Multiple periods |
