Decomposing expected fixed-income returns allows an investor to differentiate among several important return components. At the most general level, expected returns (denoted as E(R) below) can be decomposed (approximately) in the following manner:
- E(R) ≈ Yield income + Roll down return + E(Change in price based on investor’s views of yields and yield spreads) − E(Credit losses) + E(Currency gains or losses)
Yield Income
Yield income is the income that an investor receives from coupon payments relative to the bond’s price as well as interest on reinvestment income. Assuming there is no reinvestment income, yield income equals a bond’s annual current yield.
Yield income (or Current yield) = Annual coupon payment/Current bond price
Rolldown Return
The rolldown return equals the bond’s percentage price change assuming an unchanged yield curve over the strategy horizon. Bonds trading at a premium to their par value will experience capital losses during their remaining life, and bonds trading at a discount relative to their par value will experience capital gains during their remaining life.
To compute the rolldown return, the bond has to be revalued at the end of the strategy horizon assuming an unchanged yield curve. Then the annualized rolldown return is as follows:
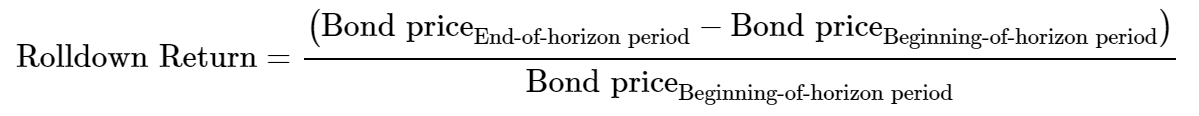
Expected Change in Price
The expected change in price based on investor’s views of yields and yield spreads reflects an investor’s expectation of changes in yields and yield spreads over the investment horizon. This expected change is zero if the investor expects yield curves and yield spreads to remain unchanged. Assuming the investor does expect a change in the yield curve, this expected return component is computed as follows:
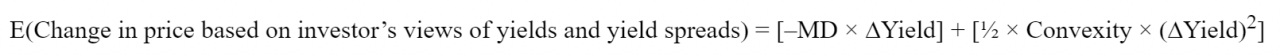
where:
MD is the modified duration of a bond
∆Yield is the expected change in yield based on expected changes to both the yield curve and yield spread
convexity estimates the effect of the non-linearity of the yield curve
Expected Credit Losses
Expected credit losses represent the expected percentage of par value lost to default for a bond. The expected credit loss equals:
- bond’s probability of default (also called expected default rate) multiplied by its expected loss severity (also known as loss given default).
Expected credit losses may be low based on past experience of default rates and resulting credit losses.
Expected Currency Impact
If an investor holds bonds denominated in a currency other than her home currency, she also needs to factor in any expected fluctuations in the currency exchange rate or expected currency gains or losses over the investment horizon.
