In an interest rate swap, a fixed rate is set so that the present value of the floating-rate payments is equal to the present value of the fixed-rate payments. This is called the swap fixed rate. If market rates increase during the swap period, the fixed rate payer will take on an increase in the swap value.
The swap fixed rate is based of Libor curve in corresponding swap tenors. To calculate the SFR, we must calculate the discount factor (Z) for each relevant Libor rate, and then calculate the SFR from those discount factors.
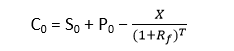
For the exam we may be asked to value an interest rate swap on settlement dates after its initiation. As noted, as rates change, the swap can take on positive or negative value for each party of the transaction. The value of the swap is the present value of the difference in payments.
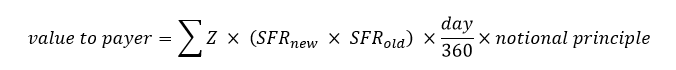
where:
∑Z = the sum of discount factors associated with the remaining settlement periods
days = number of days in the settlement period
For an equity swap we use the same SFR calculation, and then calculate the value of the underlying equity and the value of the fixed rate payments.
A swap of returns on two different stocks can be viewed as buying one stock (receiving the returns) and shorting an equal value of a different stock (paying the returns). There is no “pricing” at swap initiation, and we can value the swap at any point in time by taking the difference in returns (since the last payment date) times the notional principal.
