We can apply binomial trees to calculate the value of options. Options generate tree paths by the 2 states that can occur, an up value and a down value. To calculate the value of the option, we first adjust the up and down values in to risk neutral probability rates. If not given, the up and down factors can be calculated as:
- up factor is u = S+/S
- down factor d = S-/S
The risk neutral up probability is:
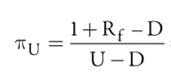
- And down factor probability is 1- up factor probability.
With these probabilities, the next step is to construct the binomial tree with the profit values and price values. To do so we find the S+ and S- terms, as well as the C+ and C- terms.
- S+ = Spot Price x Up Factor
- S- = Spot Price – Down Factor
- C+ = max profit given S+
- C- = Max profit given S-
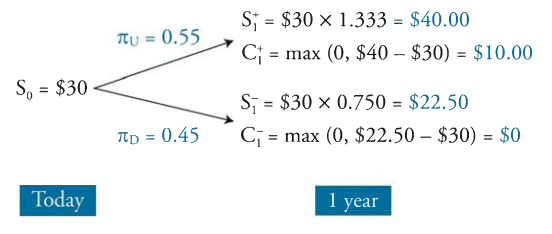
The expected value of the option is then
- (C+ x Up probability) + (C– x Down Probability)
To get the PV we discount by Rf.
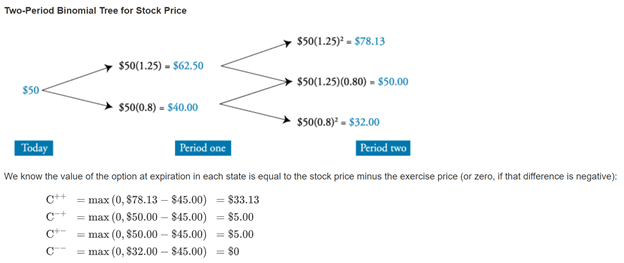
This concept can be applied to multiperiod options as well:
- Calculate the stock values at the end of two periods (there are three possible outcomes, because an up-then-down move gets you to the same place as a down-then-up move).
- Calculate the three possible option payoffs at the end of two periods.
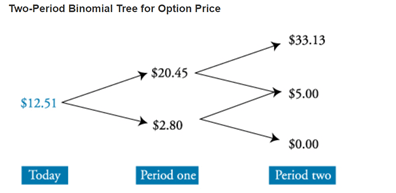
- Calculate the expected option payoff at the end of two periods (t = 2) using the up- and down-move probabilities.
- Discount the expected option payoff (t = 2) back one period at the risk-free rate to find the option values at the end of the first period (t = 1).
- Calculate the expected option value at the end of one period (t = 1) using up- and down-move probabilities.
- Discount the expected option value at the end of one period (t = 1) back one period at the risk-free rate to find the option value today (t=0).
Put option value can also be computed using put-call parity, which recognizes that the value of a fiduciary call (long call, plus an investment in a zero-coupon bond with a face value equal to the strike price) is equal to the value of a protective put (long stock and long put):
S0 + P0 = C0 + PV(X)
