he Singer-Terhaar model is based on two versions of the international Capital Asset Pricing Model (CAPM): one in which global asset markets are fully integrated, and another in which markets are fully segmented. The model then looks at the expectations of actual segmentation/integration and takes a weighted average of the two assumptions to calculate returns. The Singer-Terhaar approach begins with the CAPM:
Ri = Rf + βi,M (RM – Rf), or alternatively RPi = βi,M × RPM
where:
Ri = expected return on asset i
Rf = risk-free rate of return
βi,M = sensitivity (systematic risk) of asset i returns to the global investable market
RM = expected return on the global investable market
RPi = the asset’s risk premium
RPM = the market’s risk premium
We can manipulate this formula to solve for the risk premium on a debt or equity security using the following steps:
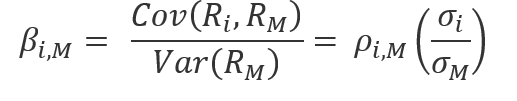
where:
ρi,M = correlation between the returns on asset i and the global market portfolio
σi = standard deviation of the returns on asset i
σM = standard deviation of the returns on the global market portfolio
Cov(Ri, Rm) = covariance of asset i return with the global market portfolio return
Rearranging the CAPM, we arrive at the expression for the risk premium for asset i, RPi:
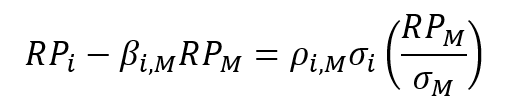
This expression states that the risk premium for an asset is equal to the product of its correlation with the global market portfolio and the standard deviation of the asset, multiplied by the Sharpe ratio for the global portfolio (in parentheses).
The Singer-Terhaar model then adjusts the CAPM for market imperfections, such as segmentation.
We will adjust for partial market segmentation by estimating an equity risk premium assuming full integration and an equity risk premium assuming full segmentation, and then taking a weighted average of the two. Under the full segmentation assumption, the relevant global portfolio is the individual asset as its own market portfolio, meaning that the asset is perfectly correlated with itself (βi,M = ρi,M = 1).
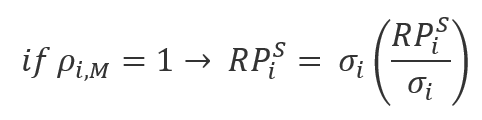
If no local market Sharpe ratio is given, then use the global market Sharpe ratio.
The last piece is to take a weighted average of the two risk premiums (calculated under full integration and full segmentation) to calculate the asset’s risk premium:
RP =φRPG + (1 − φ)RPS
where φ measures the degree of the asset’s integration with the global markets, and the superscripts are G (globally integrated) and S (segmented).
To implement the model, the analyst must supply values for the Sharpe ratios in the globally integrated market and the asset’s segmented market; the degree to which the asset is globally integrated, denoted by φ; the asset’s volatility; and the asset’s β with respect to the global market portfolio. A pragmatic approach to specifying the Sharpe ratios for each asset under complete segmentation is to assume that compensation for non-diversifiable risk (i.e., “market risk”) is the same in every market. That is, assume all the Sharpe ratios equal the global Sharpe ratio.
In practice, the analyst must make a judgment about the degree of integration/segmentation—that is, the value of φ in the Singer–Terhaar model. With that in mind, some representative values that can serve as starting points for refinement can be helpful. Developed market equities and bonds are highly integrated, so a range of 0.75–0.90 would be reasonable for φ. Emerging markets are noticeably less integrated, especially during stressful periods, and there are likely to be greater differences among these markets, so a range of 0.50–0.75 would be reasonable for emerging market equities and bonds.
