Investment approaches can also vary according to whether the manager is highly benchmark-aware or is benchmark-agnostic (i.e., pays little attention to the benchmark). Each manager will specify the acceptable levels of deviation from the benchmark, and quantify this deviation in terms of Active Share and active risk.
Active Share and active risk do not always move in tandem. A manager can pursue a higher Active Share without necessarily increasing active risk (and vice versa).
Active Share
Active Share measures the degree to which the number and sizing of the positions in a manager’s portfolio are different from those of a benchmark:
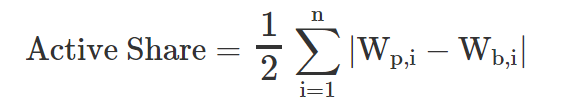
where:
n = total number of securities in the benchmark or the portfolio
Wp,i = weight of security i in the portfolio
Wb,i = weight of security i in the benchmark
Active Share takes a value between 0 and 1. If a manager holds a portfolio of stocks that are not in the benchmark, their Active Share equals 1, whereas if they hold the benchmark weights in their portfolio their Active Share will be 0.
Active Risk
Active risk, also called tracking error, is the standard deviation of active returns (portfolio returns minus benchmark returns).
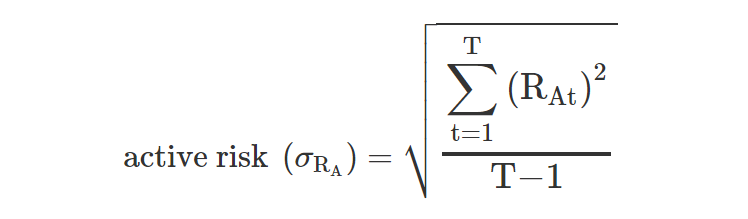
where RAt is the active return at time t, and T is the number of return periods.
There are two different measures of active risk. One is realized active risk, which is the actual, historical standard deviation between the portfolio return and the benchmark return. The other is predicted active risk, which requires forward-looking estimates of correlations and variances.
Active risk is affected by the degree of cross-correlation between securities, whereas Active Share is not.
A portfolio manager can completely control Active Share because they control the weights of the securities in the portfolio. However, a manager cannot completely control active risk because predicted active risk depends on estimations of correlations and variances of securities that may be different from those actually realized.
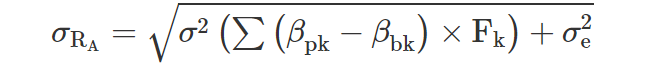
Decomposition of Active Risk
Here, we show that the active risk of a portfolio (σRA) is a function of the variance attributed to the factor exposure σ2(∑(βpk−βbk)×Fk) and of the variance attributed to the idiosyncratic risk (σ2e).
Research conclusions on the composition of active return include:
- High net exposure to a risk factor leads to high level of active risk.
- A portfolio with no net factor exposure will have active risk attributed entirely to Active Share.
- Active risk attributable to Active Share is inversely proportional to the number of securities in the portfolio.
- Active risk increases as factor and idiosyncratic risk levels increase.
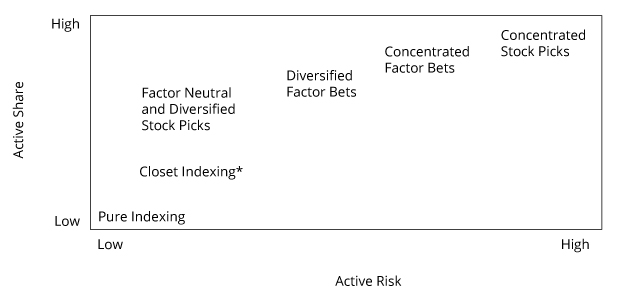
Distinguishing Between Different Portfolio Management Approaches
| Investment Style | Description | Active Share and Active Risk |
|---|---|---|
| Pure indexing | No active positions: portfolio is equal to the benchmark | Zero Active Share and zero active risk |
| Factor neutral | No active factor bets—idiosyncratic risk low if diversified | Low active risk—Active Share low if diversified |
| Factor diversified | Balanced exposure to risk factors and minimized idiosyncratic risk through high number of securities in portfolio | Reasonably low active risk—high Active Share from large amount of securities used that are unlikely to be in the benchmark |
| Concentrated factor bets | Targeted factor bets—idiosyncratic risk likely to be high | High Active Share and high active risk |
| Concentrated stock picker | Targeted individual stock bets | Highest Active Share and highest active risk |
Approaches and Their Use of Building Blocks