Duration is the sensitivity of the price of a bond or portfolio to a change in interest rates. Unlike time to maturity duration is not a linear concept. Holding all other variables constant, duration tells us how long we need to hold a bond to realize the yield from time of purchase.
Duration can be used in immunization strategies, indexing strategies or active strategies.
Immunization and indexing strategies involve concepts around of matching duration – either to liabilities or an benchmark index. Immunization specifically is the the process of creating a portfolio that will minimize the variance in the realized rate of return in a known time horizon.
Duration matching aims to match the duration of assets to duration of liabilities. The core principle is that duration matched assets and liabilities should behave similarly in the face of interest rate changes, leading to no net change in the the value of assets or liabilities.
Two conditions for duration matching are:
- The duration of the asset portfolio should equal the duration of the liability portfolio.
- The PV of assets must equal the PV of the liabilities.
Duration matching is premised on certain assumptions and conditions. Portfolios are only matched at a given point in time. Rebalancing is required to maintain the match. Immunization also ignores credit quality and default risk. If bonds have optionality, effective duration must be used.
Effective duration is the sensitivity of a bond’s price to a change in a benchmark yield curve. Effective duration allows us to take into account the fact that bonds with options can have their cash flows altered. We also need to use effective duration when the liability is Type II, III and IV.
The solution to a basic immunization problem for a single liability would be to by a matching zero coupon bond that has the same maturity as the obligation. (Implying our liability is similar to being short a zero coupon bond). Given the absence of a perfect offsetting zero coupon bond, we can leverage the concept of Macaulay duration to immunize our asset’s reinvestment and price risk by having them offset each other.
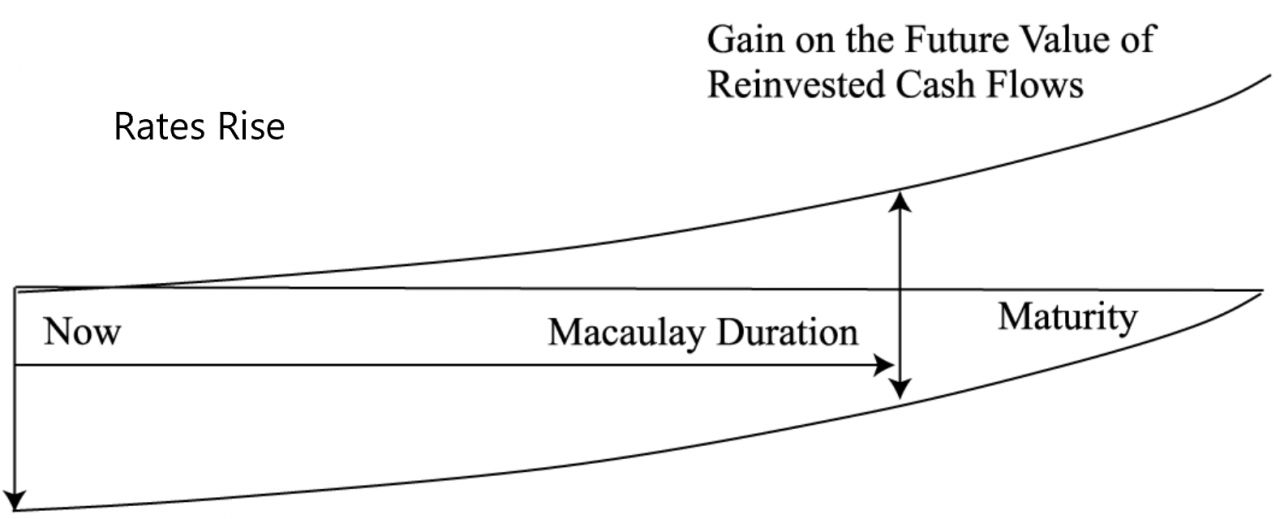
Macaulay duration is the weighted average time until the cash flows of an instrument recoup the initial outlay, given the case of a parallel shift in the yield curve (as shown above as the point when reinvested cash offsets loss in price). It is a measure of time. That is why the Macaulay duration of a zero-coupon instrument is its maturity, but Macaulay duration of a non-zero-coupon instrument is less than its maturity. The assumption here is that coupons will be reinvested, thus the time to realize the initial market discount rate on a bond should be shorter than the full maturity of the bond.
The three principles of immunizing a single liability can be as follows:
- MacDur of assets = MacDur of liabilities
- PV of assets is greater than or equal to PV of liabilities
- Portfolio convexity is minimized
- For a single liability, this reduces the risks of non-parallel yield curve shifts and twists offsetting the duration matching.
As we move into immunizing multiple liabilities and introduce structural changes in the yield curve (as opposed to one time parallel shifts), we must update our conditions using different measures of duration. When using coupon paying assets against multiplied liabilities, we must factor in convexity of our portfolio vs the convexity of our assets. In this situation, it because better to use money duration (also known as dollar duration) as our duration measure.
Money duration (Dollar Duration): Money duration is the dollar change in value of the assets or liability for change in interest rates. It can be calculated as modified duration (MD) multiplied by the value of the item multiplied by a specified change in yield of the item. It is common to express it as basis point value (BPV):
BPV = MD × V × 0.0001 = price value of a basis point
Modified duration is Macaulay duration divided by 1 plus the periodic interest rate used to compute the cash flow PVs:
- Modified duration is the (slightly) more accurate measure of immediate price change of the instrument.
- Macaulay duration is the (slightly) more appropriate measure of time for some immunization techniques.
Modified duration can be thought of as the duration expressed in percentage form.
With these concept we can rewrite the requirements regarding immunization as:
- DD of assets = DD of liabilities
- Or can convert DD to BPV
- PV of assets is greater than or equal to PV of liabilities
- Convexity of assets is greater than convexity of liabilities
For indexing, the primary use of duration is as a risk factor of the benchmark to be matched. Modified duration, effective duration and option adjusted durations are all considered risk factors that would ideally be matched.
This introduces key rate duration as well. Key rate duration is a measure of a bond’s sensitivity to a change in the benchmark yield curve at a specific maturity point or segment. By effectively matching the key rate durations between the portfolio and the underlying index, a manager can significantly reduce the portfolio’s exposure to changes in the yield curve.
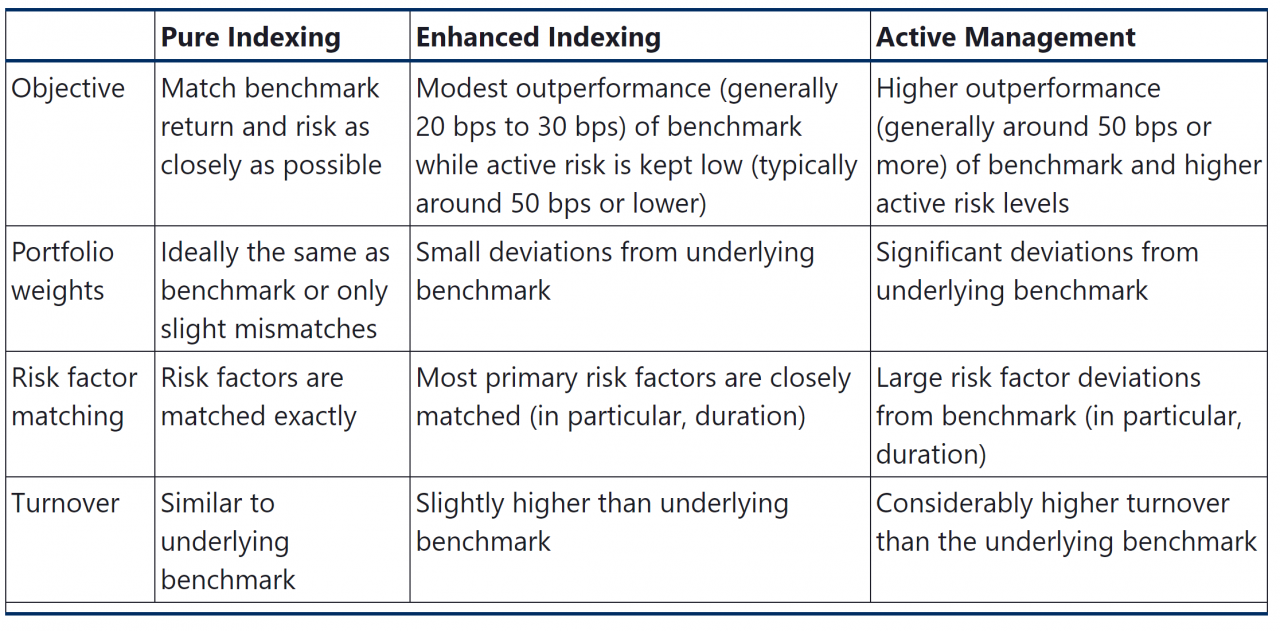
Key rate durations can be used to identify bullet and barbell term structures.
