In reading 10, the curriculum introduces the following equation. The equation ties the trend growth rate to the value of equity.
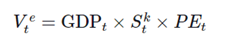
The above states: value of equity is equal to the level of nominal GDP times the share of profit in the economy times the PE ratio. In the long run, the capital’s share of income and the PE approach zero as they cannot continuously increase or decrease. Hence the value of equity in the long run is linked to the growth rate of nominal GDP.
This gives us the “capital appreciation” component of equity returns. However, there is also the dividend yield that needs to be accounted for in the value of equity. That lends to the following implied equation:
E(Re) = Ve + Dt = value of equity plus the dividend yield.
We can see that this equation above is essentially the same as the Gordon Growth model:
R = D/P + g.
G is the the capital appreciation component, which in the long run is the trend rate of nominal GDP growth.
We can also tie these concepts back to the Grinold-Kroner model, which is a measure of the short-run or finite horizon expected return on equity. Or rather we can see how the Grinold-Kroner model is really just an expansion on the Gordon Growth model:
E(Re) ≈ (D/P − %ΔS) + %ΔE + %ΔP/E
In the long run we can see that the change in PE and Share buy backs will tend towards zero, as they cannot continuously increase or decrease. In this case we are left with
E(Re) ≈ D/P + %ΔE
We know in the long run that the change in expected earnings will tend towards the nominal GDP growth rate.
Therefore we are lead back to:
E(Re) ≈ D/P + g
