Covered interest rate parity is the condition in which forward premiums or discounts are offset by interest rate differences between the currencies.
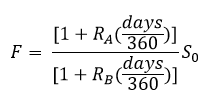
where:
F = forward rate (quoted as A/B)
S0 = spot rate (quoted as A/B)
days = number of days in the underlying forward contract
RA = interest rate for Currency A
RB = interest rate for Currency B
From this we can derive the forward premium or discount equation

Uncovered interest rate parity is the same idea as covered rate parity, but refers to situations where arbitrage is not possible, such as currencies with no available forwards or governed by capital controls.
E(%ΔS)(A/B) = RA − RB
Comparing covered and uncovered interest parity, we see that covered interest rate parity derives the no-arbitrage forward rate, while uncovered interest rate parity derives the expected future spot rate (which is not market traded). Covered interest parity is assumed by arbitrage, but this is not the case for uncovered interest rate parity.
