MM I is a theory that shows that the value of a firm is not affected by the firms capital structure. This is said to hold true in a hypothetical world where there are no taxes, capital markets are perfectly competitive, investors have homogeneous expectations, riskless borrowing and lending exists, no agency costs exist, and investment decisions are not affected by financing decisions.
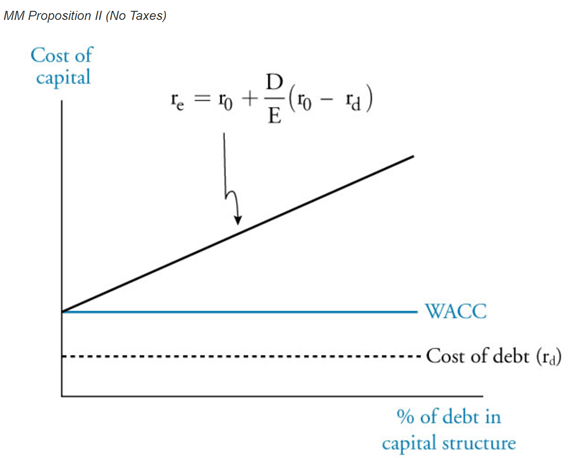
Using the same set of assumptions, MM II states that the cost of equity increases linearly with increases in the ratio of its debt financing. Therefore, the benefits of using a larger proportion of debt as a cheaper source of financing are offset by the rise in the cost of equity, resulting in no change in the firm’s weighted average cost of capital (WACC). We can derive this theory from the WACC formula:
where:
re = required rate of return on equity, or cost of equity
r0 = company unlevered cost of capital (i.e., assume no leverage)
rd = required rate of return on borrowings, or cost of debt
If we add taxes to MM I, we introduce the concept of a tax shield, which leads to being 100% debt financed as the optimal capital structure. This is because in most countries, interest payments are tax deductible.
The value the tax shield adds can be shown thus:
VL = VU + (t × d)
where:
VL = value of levered firm
VU = value of unlevered firm
t = marginal tax rate
d = value of debt in capital structure
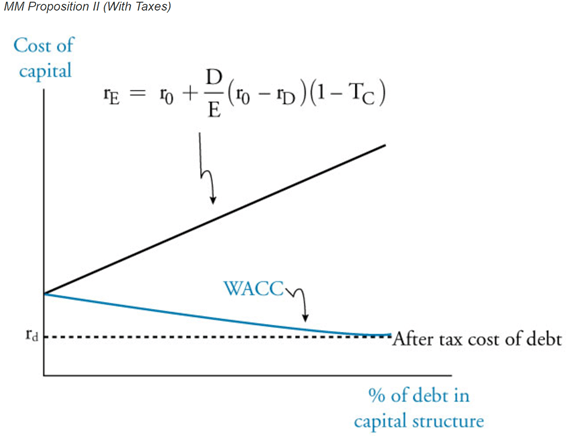
In the same vein, we see that introduces taxes to MM II alters the proposition so that increasing debt causes the WACC of a firm to decline. WACC is minimized when a company is 100% debt financed.
where:
re = required rate of return on equity, or cost of equity
r0 = company unlevered cost of capital (i.e., assume no leverage)
rd = required rate of return on borrowings, or cost of debt
TC = tax rate