The information ratio is made up of three components, the information coefficient, which is an ex-ante measure of manager skill. There is also an ex post information coefficient, and generally speaking the IC can be defined as the risk-weighted correlation between active returns and forecasted active returns.
The transfer coefficient which is the correlation between actual active weights and optimal active weights, and breath, the number of active independent bets taken per year.
In an unconstrained portfolio, we have a TC of 1 and can calculate optimal portfolios with the following:
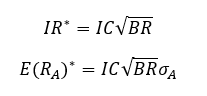
In a constrained portfolio the transfer coefficient will be less than one as the optimal weights will differ from the actual weights. We must adjust the previous two equations for this:
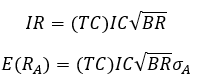
Since transfer coefficients are always less than one in this case, the information ratio will be less than the optimal information ratio and the expected active return must be less than the optimal expected active return.
To calculate optimal risk used in the equation above, we take function of the information ratio, the Sharpe ratio and the standard dev of benchmark return:
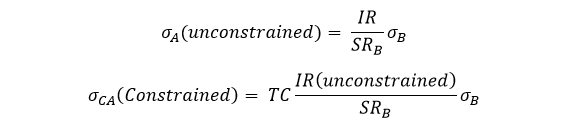
For the Sharpe ratio, we have a similar constrained ratio which will be lower than its unconstrained counterpart:
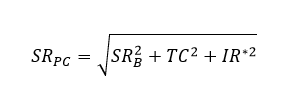
Realized value added from active management is the ex-post alpha that the manager achieves. Using the ex-post information coefficient ICR, the fundamental law can be written as:
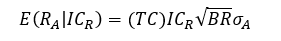
The actual return on the active portfolio can be expressed as its conditional expected return and a noise term:
RA = E(RA | ICR) + noise
Where:
E(RA | ICR) represents the expected value added, given the skill of the investor that period.
The proportion of realized variance attributed to variation in the realized information coefficient is TC2.
