- Delta (Δ) is the change in an option’s price in response to a change in price of the underlying, all else equal. Delta provides a good approximation of how an option’s price will change for a small change in the underlying’s price. Delta for long calls is always positive; delta for long puts is always negative. Delta (Δ) ≈ Change in value of option/Change in value of underlying.
- Gamma (Γ) is the change in an option’s delta for a change in price of the underlying, all else equal. Gamma is a measure of the curvature in the option price in relationship to the underlying price. Gamma for long calls and long puts is always positive. Gamma (Γ) ≈ Change in delta/Change in value of underlying.
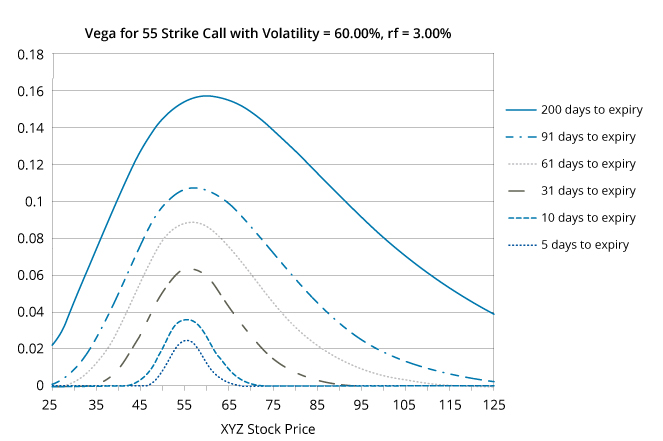
- Vega (ν) is the change in an option’s price for a change in volatility of the underlying, all else equal. Vega measures the sensitivity of the underlying to volatility. Vega for long calls and long puts is always positive. Vega (ν) ≈ Change in value of option/Change in volatility of underlying.
- Theta (Θ) is the daily change in an option’s price, all else equal. Theta measures the sensitivity of the option’s price to the passage of time, known as time decay. Theta for long calls and long puts is generally negative.
Delta and Gamma
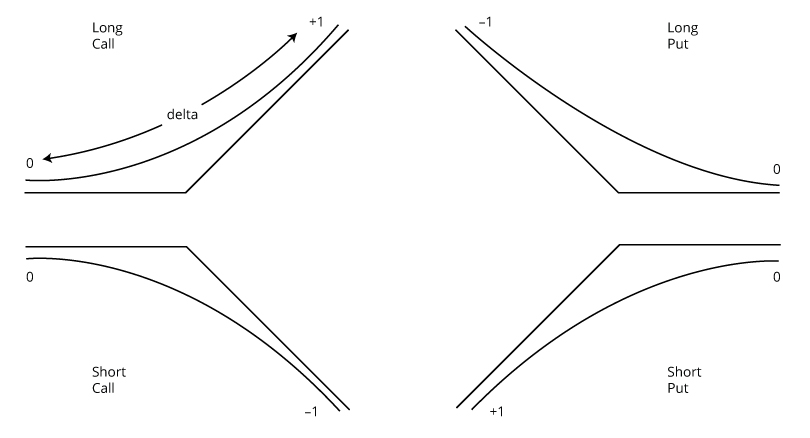
Puts (long) have negative delta, since the line slopes downwards, but there is a simple rule that applies to both calls and puts regarding the absolute size of delta (i.e. ignoring the sign):
All other factors held constant:
- The more ITM is an option, the higher is its (absolute) delta (closer to 1).
- The more OTM is an option, the lower is its (absolute) delta (closer to 0).
The following diagram summarizes the ranges of values of delta for long and short calls and puts:
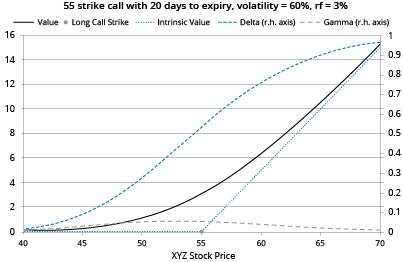
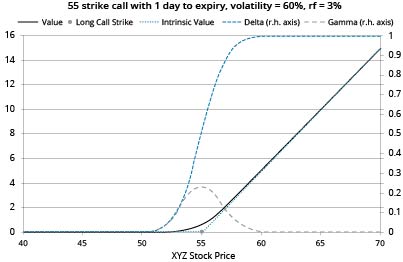
Gamma is trickier to generalize, but it tends to be higher the closer to ATM an option, and is at its greatest for ATM options that are close to expiration. For instance, the following graphs illustrate the same call, first with 20 days to expiration and then with one day to expiration when, with much less time remaining (so much less time value), the option premium line is crammed into a narrow range either side of the strike price, so gamma is highest over that range:
Deltas for the Underlying and for Futures and Forwards on the Underlying
It follows directly from the definition of delta that:
- The delta of a long position in one unit of the underlying is +1.
- The delta of a short position in one unit of the underlying is -1.
Futures and forwards on underlyings that pay no yield (e.g. nondividend paying stocks) are essentially proxies for the underlying, so they also have deltas of +1 (if long) and -1 (if short). All the examples we consider in this reading use underlyings of this sort.
Theta and Vega
Theta measures how quickly an option loses value as time passes.
Theta changes as the time passes. Options that are close to ATM have the highest thetas (in absolute terms), and these increase as expiration approaches (all other factors being held constant). In other words ATM options lose time value at an increasing rate as they mature. Here is an illustration, the horizontal axis is number of days to expiry, and the vertical axis is time value:
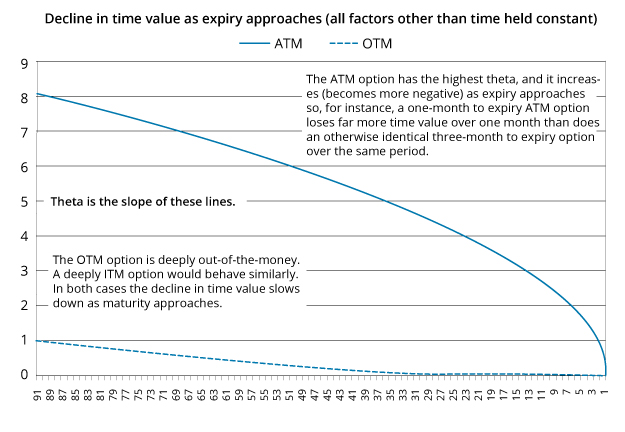
Vega measures the effect of a 1% increase in volatility on the value of the option.
Vegas are always positive: a more volatile underlying makes all the options on it more valuable (because there is more uncertainly about how things will turn out at expiration, thus more time value).
All other factors constant, vega is higher the more time there is to expiry, but it diminishes the further ITM or OTM the option is. For example: