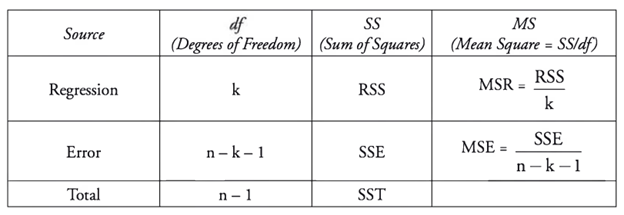
ANOVA
Table 1: CFA Anova Model
ANOVA is short for analysis of variance. The key concept are sum of squared deviations. The goal is to dig into the differences between observed values, observed mean and our regression line.
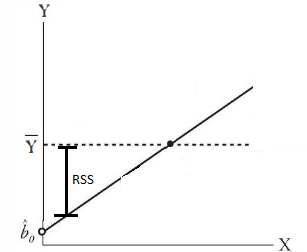
The Total Sum of Squares, or SST is the sum of the deviations of each observed value from the population mean. For example, given observed values of 1, 2, 3 we have a population mean, or simple average of 2. SST is also two in this case, as SST = (2-1) + (2-2) + (3-2) = 2.
The regression sum squared, or RSS is the difference between each point of the regression line of our model and the population mean. In the example above, because we have a linear equation that fits the observed points perfectly (y = x), the RSS = SST. This is called the explained variation, because it is variation from the population mean that our model (line) explains.
Moving onto the residual sum of square errors, or SSE, we have the sum of the differences between the observed values and the regression line. Consider if the observed values where 1.2, 2, 2.8, our linear regression line would likely still be y = x. This means the population mean would still be 2 and the RSS would still be two as well, since our model is assumed to not have changed. However, now we cannot say that RSS = SST, because the observed values are no longer perfectly on the regression. There is an additional variation between the observed value and the linear regression line. This is the SSE, and SST = RSS + SSE. SSE is also known as unexplained variation, as it lies outside of what is predicted by our regression line. In an optimized regression, the lower the SSE, the better the regression fits the data.
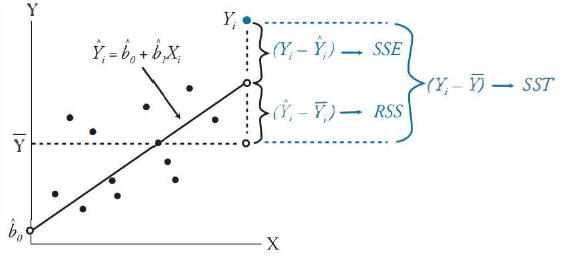
Another implication of this breakdown is that R2 = RSS/SST. We see this just means that the R2 value indicates how much of the variance between the observed value and the population mean is explained by our regression line.
From this here we can easily derive MSR and MSE – which are just means of RSS and SSE.

very clear